Beregning af parallaksemetoden

Hej Spørg om Fysik
Jeg har lidt problemer med at forstå Parallaksemetoden. Hvordan virker metoden?, hvordan kan man ved hjælp af parallaksemetoden beregne afstanden til en nær stjerne?

Hvordan bliver enheden parsec defineret? Det vanskeligste for mig at forstå, er det med bueminutter og buesekunder - hvordan det skal forstås.

Jeg har læst en del og det, og har prøvet at danne mig en forståelse, men jeg forstår det ikke. Så jeg vil blive meget glad hvis jeg får et svar, især hvis det er lidt "pædagogisk" forklaret. Håber på et svar snarest, da jeg er lidt i tidsnød.

(Det lille billede fra forrige side viser hvordan stjernen ses på baggrund af farvefirkanterne - altså parallakse med synet)

På forhånd tak!

Med venlig hilsen
A.K.V

Ser man på en genstand i ca. 1 meters afstand, og holder skiftevis en hånd for det ene øje og det andet øje, så ser man, at genstanden synes at bevæge sig i forhold til baggrunden.

Det er parallakse, og det skyldes at vores øjne på en voksen sidder i en afstand på 6-8 cm (normalt). Vi bruger det til at bestemme afstande til ting, der er forholdsvis nær på os - det vil sige i meterområdet. Ordet stammer fra græsk og kan bl.a. betyde at skifte. Vi har andre metoder på store afstande, hvor vi f.eks. bruger vores viden om tings virkelige størrelse, erfaring mm. Hvis man vil se, at det er afstandsbestemmelsesmetoden, så stil en blyant eller en anden let ting på højkant i næsten arms afstand, og grib den med et hurtigt sving med armen. Prøv igen, men hold en hånd for det ene øje under processen (pas på man rammer måske ved siden af).

Det at ting ses forskelligt i forhold til baggrunden anvender astronomerne til at bestemme afstande til de nærmeste stjerner og til andre himmellegemer. Hvis en astronom i Florida og en i Danmark samtidigt kan se månen og fotograferer den og sammenligner dens position med fjerne stjerners, får man samme effekt og kan på den måde bestemme afstanden til månen. Her er "øjenafstanden i stedet omkring 10 000 km, og man kan derfor måle afstanden så langt borte som til månen, og længere væk. I dag måler man måneafstanden med centimeters nøjagtighed ved at måle den tid en LASER-lys puls tager frem og tilbage. På denne måde kan vi med parallaksemetoden måle afstande i solsystemet, der findes dog også en række bevægelseslove, som kan hjælpe os ud fra omløbstiden.

Jordens diameter er ikke nok, hvis man skal måle afstande til stjernerne

Vi har brug for en større "øjenafstand", en større afstand imellem fotografierne. Det får man ved at fotografere stjernerne med ½ års mellemrum dvs. afstanden er diameteren i jordens bane, denne diameter er ca. 289,2 * 10⁶ km. Faktisk tager man fotos i løbet af et år, de nærmeste stjerner ser så ud til at bevæge sig i en lille ellipse, som så er afspejling af jordbanen (det er næsten en cirkel for stjerner, der ligger vinkelret på jordbanens baneplan). Mere præcist parallaksen er den vinkel jordbanens HALVE storakse (som kaldes 1 AU = astronomisk enhed altså149,6 * 10⁶ km) ses under fra stjernen, dvs. ved målinger med ½ års mellemrum får man den dobbelte parallakse.

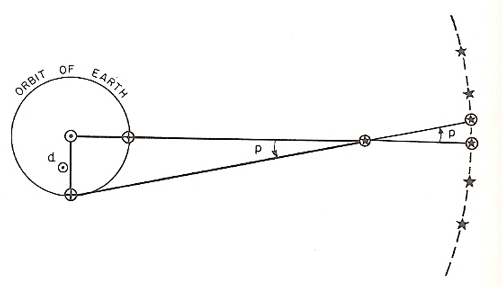
Billedet er taget fra Struves Astronomi, p er parallaksevinklen

Bueminutter og buesekunder 

På de fotos man optager måler man vinkler. En komplet omdrejning er fra gammel tid (vist Babylonerne) 360 ⁰, også fra gammel tid inddeles 1 ⁰ i 60 dele, som man kalder bueminutter. 1 Bueminut (skrives 1') inddeles i 60 dele, som man kalder buesekunder, et buesekund (skrives 1") er altså 1/3600 af 1 ⁰.

Den nærmeste stjerne fra solen ses fra den sydlige halvkugle og hedder alfa Centauri. Parallaksen til den er 0,751". Det er ikke ret meget. Hvis man beregner afstanden bliver den 4,1*10¹³ km.

Denne type af målinger har bevirket, at man har indført et nyt afstandsmål i rummet. Afstanden 1 parsec er den afstand, hvor parallaksen er 1", det kan udregnes til 3,1*10¹³ km, afstanden fra før er altså ca. 1,3 parsec. Man bruger også en anden afstandsenhed i rummet nemlig lysår dvs. den strækning, lys bevæger sig på 1 år. Det er ca. 9,5*10¹² km, så afstanden til α-centauri er altså 4,3 lysår.

Grænsen for at måle den geometriske parallakse ligger omkring 0,01" eller 100 parsec. For stjerner længere væk findes en række metoder baseret på lysstyrke eventuelt forbundet med lysstyrkevariation, statistiske metoder etc. Der er ikke nogen øvre grænse for måling af afstande, men des længere væk des mindre nøjagtige bliver mange af metoderne.

Med venlig hilsen
Jens Viggo Clausen
Malte Olsen