Bølgers udbredelseshastighed
Hej Spørg om Fysik
Ifølge Maxwells ligninger afhænger lyshastigheden kun af de elektromagnetiske ”materialekonstanter” for det medie, som lyset udbreder sig i – dvs lyshastigheden er konstant i mediet, uafhængig af lysgiverens hastighed i forhold til mediet.
Gælder der det samme for andre bølgeformer?
Med venlig hilsen
C R

Bølgers udbredelseshastighed
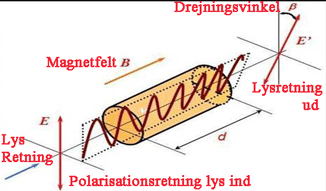
Det ses at polarisatiomsretningen drejes ved gennemgang i stof påvirket af magnetisk felt
Elektromagnetiske bølger
Elektromagnetiske bølger er tværbølger (transversalbølger) dvs. felterne (elektrisk og magnetisk) svinger vinkelret på udbredelsesretningen (akkurat som overfladebølger på vand). Man kan, ud over hvad der fremgår af normale materiale konstanter, påvirke de elektromagnetiske bølger ved udefra at pålægge stoffer der bevæger sig i et magnetfelt, det kaldes Faraday effekt. En række gennemsigtige stoffer herunder væsker, har den egenskab.
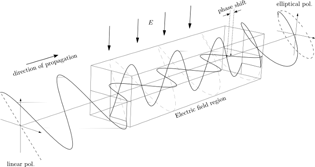
Kerr-effekt. her ses at de to polatisationsretninger har forskellige hastighed i stoffet påvirket af elektrisk felt
Man påviser det lettest i glasser dopet med en række stoffer. Det der sker, er at rotationshastigheden af polariseret lys bliver lidt forskelligt for højre- og venstre polariseret lys, altså 2 lyshastigheder for samme lysstråle, så man f.eks. kan lave et envejsvindue, hvor polariseret lys fra den ene ende i den optiske substans, med en polarisator i hver ende, kan komme igennem, men intet kommer igennem fra den anden ende. I pulsradar kan effekten anvendes på ferritstænger anbragt i bølgelederne, så der pålægges magnetfelt på bølgelederen til modtagers med feritstangen, når pulser udsendes, og åbnes når det svage reflekterede signaler kommer tilbage. Optisk er effekten lille men synlig i f.eks. svovlkulstof (væske) og blysilikatglas, i alle tilfælde, dvs. der kræves forholdsvis store magnetfelter for at få en virkning. Der findes en række specielt fremstillede stoffer, hvor effekten er betydeligt større.

Næstnederst ses tværbølger (transversalbølger) hvor svingningerne er vinkelret på udbredelsesretningen. Nederst ses længdebølger (longitudinalbølger) hvor svingningen er i udbredelsesretningen.
Tilsvarende kan et elektrisk felt på tværs af lysets strålegang påvirke lysets polarisation, det kaldes Kerr effekt. Her ændres materialets brydningsforhold af feltet dvs. igen udbredelseshastigheden af lys. Her findes en række specielle glasser med særlig stor effekt og en væske som f.eks. nitrobenzen.
Af andre bølgefænomener er de mest karakteristiske mekaniske bølger, som vi her stort set kan samle som lyd, og overfladebølger. Det er derfor disse, som bruges som eksempler nedenfor.
Lydfænomener forekommer bl.a. i luft, det er længdebølger dvs. lyden udbreder sin i samme retning som svingningerne sker (longitudinalbølge). Her kan lydhastigheden i en given luftart udtrykkes:
v2 = k*R*T/M
Hvor v er lydhastigheden, k er luftens varmefyldeforhold, k = cp/cv , R er gaskonstanten, M luftartens molvægt og T den absolutte temperatur. Hastigheden er altså temperaturafhængig, hvilket ikke er en stofkonstant. I væsker er der en ganske lille afhængighed igennem væskens sammentrykkelighedskonstant, men den kan man næsten se bort fra. Der er derimod en afhængighed af densiteten, ρ, som har en del temperaturafhængighed, men de kan vel siges at være en temperatur afhængig stofkonstant. Det er netop under temperaturlag at u-både kan gemme sig for sonar på grund af spring i lydhastigheden.
I udstrakte faste stoffer kan der være både længdebølger og tværbølger, og lydhastigheden, v, afhænger i første orden af Youngs modul (en fjederkonstant) igennem
v2 = E/ρ
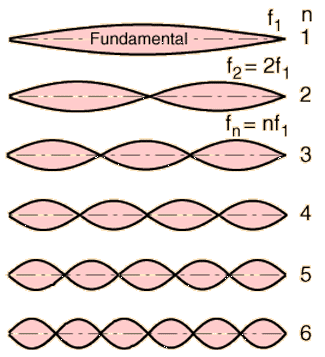
Her ses pårincipperne for en svingende streng med de tilhørende overtoner
hvor E er Youngs modul, og ρ er densiteten af stoffet. Youngs modul er normalt stort set konstant, men ved visse stoffer og store kræfter kan den være ikke lineær, og altså give afvigelser fra simple stofkonstanter, på den anden side vil ikke lineære effekter, som kan tabelleres, måske kunne siges at være en del af stofkonstanten, men det kan altså afhænge af påvirkningens størrelse. I faste stoffer kan man både have tværbølger og tværbølger.
Hvis der er tale om ikke udstrakte faste stoffer, illustreres det bedst, hvis man tænker på en stålstang med diameter 5 mm og længde 1 m. Man kan starte længdebølgen ved at slå med en hammer på enden, så udbreder en lydbølge sig til den anden ende. Transversalbølgen kan startes ved at slå med en hammer på siden. Længdebølgen breder sig med ca. 3 gange hastigheden af transversalbølgen (forskellige værdier af Youngs modul, det er lettere at bøje stangen til siden end at trække den længere), her betyder påvirkningsmåden eller retningen altså noget for udbredelseshastigheden, og dermed kan denne ikke bare beskrives ved en stofkonstant.
Snorbølger, svingninger på f.eks. en klaverstreng. Her er tale om en spændt stålstreng og tværbølger og udbredelseshastigheden kan beskrives som:
v2 = F/ρ
hvor v er hastigheden, F er kraften man trækker i strengen med og ρ er densiteten (masse pr. længdeenhed). Undersøger man imidlertid overtonerne på en klaverstreng, ser man, at de er for høje i forhold til grundtonen. Det der går galt er, at man under udledningen antager, at F er den kraft der trækker strengen tilbage til ligevægtsstillingen efter en bølgetop. Det er ikke helt rigtigt, for alle der har haft et stykke pianotråd i hånden ved, at den krummer rundt, selv om man søger at rette den ud.

Overfladebølger
Det betyder, at kraften for at få tråden tilbage så den bliver lige, er større end trækkraften F. Des kortere bølgerne bliver des større effekt har den virkning. Man kan finde udbredelseshastigheden vokser med stigende frekvens og f.eks. kan hastigheden når bølgen bliver 10 gange kortere være omkring 10 % højere (afhængig af strengen mm.). Udbredelseshastigheden er altså frekvensafhængig. Det var denne frekvensafhængighed der gjorde, at det tog så mange år at få elektroniske keyboards til at kunne lyde som et klaver (i modsætning til de fleste andre instrumenter).
Overfladebølger er tværbølger. Her er vand et glimrende eksempel, det kender vi alle. Man kan vise, at overflade bølgers hastighed har formen (med visse tilnærmelser):
v2 = (g/k + C*k/ρ) *tanh(kh)

Bølger som kommer på lavt vand og hvor toppen "løber fra" bunden
hvor g er tyngdeaccelerationen, k = 2*π/λ dvs. afhængig af λ som er bølgelængden, C er overfladespændingen af vandet (det der gør at insekter kan gå på en vandoverflade), ρ er densiteten, h er vanddybden. Tanh() er en matematisk funktion. Her er hastigheden altså afhængig af bølgelængden i flere led i formlen igennem k. Desuden overfladespændingen f.eks. sæbe giver en drastisk ændring af bølgehastigheden, af h altså vanddybden. Den sidste afhængighed er den der gør, at bølger kammer over, når de når en revle, så bliver der en stor vanddybde under bølgetoppen og en mindre for bølgebunden, altså toppen bevæger sig hurtigere end bunden, og derfor ”falder den ned” foran bølgen. Det har naturligvis ikke betydning på dybder meget større end bølgehøjden.

Kølvand efter svaner med større fart end bølgehastigheden
I luft og på vand kan man endvidere have kølvand, hvor f.eks. i vand, en svømmende svane (eller et skib) har kølvand i V- form bag sig, når den bevæger sig hurtigere end bølgehastigheden, det gør kølvandet så også, det tilsvarende fænomen i luft er det supersoniske brag fra et overlydsfly, som også er et ”kølvand”.

Chokbølger ved afskydning af et skydevåben, fotograferet ved en særlig teknik
I de overstående tilfælde forudsættes, at de enkelte massedele vender tilbage til ligevægtsstillingen, når bølgen er forbi, og at gassen eller væsken er i ligevægt bagefter (det gælder ikke helt for kølvand).
Det er ikke opfyldt for meget voldsomme effekter f.eks., visse eksplosioner, hvor trykbølgen fra eksplosionen i første omgang netto flytter større luftmængder. Lydhastigheden i luft er omkring 330 m/s, i nærheden af et sprængningssted vil der de første måske 10 m være trykbølgehastigheder på 500 – 10 000 m/s, afhængig af ladningens størrelse. Den aftager så til det normale med afstanden.
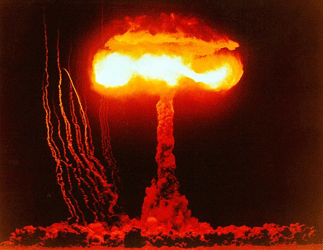
Atomvåbensprængning. stregerne til højre er raktter affyret for at se chokbølgen
Store eksplosioner dvs. atomvåben se bl.a.: Trykbølger fra A-våben >> har tilsvarende effekter nær våbnet (nær kan måles i kilometer), men chokbølgen kommer ret hurtigt ned i hastighed til omkring normal lydhastighed. Trykbølgen fra større atomvåben kan sagtens vælte huse på afstande af 10 km.
Der er altså mange steder også flere end de nævnte, hvor bølgehastigheden ikke simpelt kan bestemmes ud fra materialekonstanter.
Med venlig hilsen
Malte Olsen
