Centripetalkraft og centrifugalkraft
Hej Spørg om Fysik
Jeg er en 17 årig pige der går på HTX. Vi har om kræfter lige nu, og jeg har et par spørgsmål, men siden det ikke er pensum, vil min lærer ikke gå i dybden med det.
Jeg forstår ikke forskellen mellem centrifugalkraften og centripetalkraften. I min fysikbog står der at centrifugalkraften slet ikke findes, men bare er 'en følelse'. Samtidigt skriver de at centripetalkraften og centrifugalkraften ophæver hinanden, men at centripetalkraften findes. Hvordan kan en kraft der ikke findes ophæve en kraft der findes?
Når de beskriver centrifugalkraften som en 'følelse', med eksemplet at når man sidder på en karrusel der drejer, bliver man tvunget udaf, væk fra omdrejningspunktet. Deres forklaring er, at grunden til denne følelse, er fordi du ikke selv er en del af karrusellen. Men hvad så hvis jeg lagde en ting, fx en bog, på karrusellen og drejede den hurtigt nok rundt - så ville bogen da til sidst 'flyve' af? Jeg kan ikke forstå hvordan centrifugalkraften så ikke findes, men kun er en 'følelse', når man kan se at bogen falder af...
Mange tak på forhånd
Hilsen L.

Kære L. , det var et knaldgodt spørgsmål. Nej, centrifugalkraft og centripetalkraft ophæver ikke hinanden uden videre, og de er principielt to helt forskellige ting.
Først lige lidt baggrund med Newtons tre love:
Den første lov siger, at legemer der ikke påvirkes af kræfter udefra, vil forblive i den tilstand de er, enten ligge stille eller bevæge sig retlinet med konstant hastighed. Den kaldes inertiens lov og et koordinatsystem, hvor den gælder, kaldes et inertialsystem.
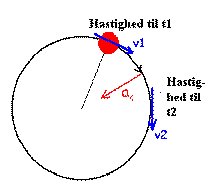
Centripetalaccelerationen imod centrum
Anden lov siger, at i et inertialsystem gælder, at kraft F og acceleration a er proportionale (proportionalitetskonstanten m er massen) og går i samme retning: F = ma. De bogstaver der er fede betyder vektorer, dvs. størrelser med retning (pile).
Tredje lov siger, at hvis to legemer påvirker hinanden med kræfter, er disse kræfter lige store og modsat rettede (de ophæver ikke hinanden, fordi de virker på to forskellige legemer), kræfterne kaldes ofte aktion og reaktion.
Det vi omtaler som kraft, skal komme et eller andet sted fra; der er en årsag, en fysisk lov bagved en kraft. Det kan være tyngdekraften, og det kan være elektriske, magnetiske, fjederkræfter, kræfter fra bjælker og tove eller mangfoldige andre ting, men i inertialsystemer kan vi altid pege på fysiske årsager til kræfterne. Et eksempel på aktion og reaktion kunne være tyngdekraften, som Jorden påvirker dig med, og den (tyngde)kraft, som du trækker i Jorden med; de er lige store og modsat rettede (helt præcist dog kun ved polerne).
Nu til cirkelbevægelse.
Centripetalkraft
Hvis vi står i laboratoriet (et inertialsystem) og kikker på en partikel, der gennemløber en cirkelbevægelse, er det klart, at partiklen ikke bevæger sig i en ret linje med konstant hastighed. Det betyder altså, at partiklen har en acceleration og dermed må være påvirket af en kraft, ifølge anden lov. I en cirkelbevægelse kaldes denne kraft centripetalkraften, den ”midtsøgende kraft”. Kraften er rettet imod centrum, fordi accelerationen ret let med lidt geometriske overvejelser kan ses at være rettet imod centrum. Indfører man vinkelhastigheden, ω, som er vinklen i buemål pr. tidsenhed, kan man se, at den hænger sammen med omløbstiden T, som omkredsen af en enhedscirkel (en cirkel med radius 1) i buemål, som er 2 π, divideret med tiden, altså ω = 2 π/T. Accelerationen i cirkelbevægelsen kan vises at være a = rω 2, hvor r er radius, og den er altså rettet imod cirklens centrum.
Centrifugalkraft
Vi nu sætter os nu på en karrusel, der roterer, og ser på en klods med massen m ude ved karrusellens kant. Set fra karrusellen ligger massen stille, og er ikke accelereret.

Svingkarrusel, kæderne leverer centripetalkraften
Hvis vi vil kunne bruge Newtons anden lov i dette roterende system, må vi konkludere, at den resulterende kraft på massen er nul. En kraftmåler mellem klodsen og karrusellen ville imidlertid vise, at karusellen påvirker m med en kraft indefter på F = m r ω2 (centripetalkraften i laboratoriesystemet). Der må således virke endnu en kraft af samme størrelse udefter. Det er den, vi kalder centrifugalkraften, ”kraften, der flygter fra centrum”. Man kalder den en fiktiv kraft, fordi der ikke er en fysisk kraftlov, der fremkalder den, men den føles meget virkelig i sådan et roterende system, og vi bruger den i centrifuger til at tørre tøj, i karruseller til underholdning osv. Hvis vi imidlertid prøver at rulle med en kugle på karrusellen, kan vi se, at Newtons første lov ikke er opfyldt, vi befinder os ikke i et inertialsystem. Kuglen bevæger sig ikke i en ret linje med konstant hastighed, men i en krum kurve efterhånden med stigende hastighed (set fra laboratoriet følger kuglen faktisk en ret linie, og karussellen løber bare væk under den). Genstande på karrusellen er underkastet en acceleration i forhold til karrusellen, åbenbart uden at der set fra karrusellen er årsag til en kraft, og den tredje lov siger jo, at der ved kræfter i inertialsystemer er to legemer indblandet, og at de påvirkes af hver sin kraft, som er lige store og modsatrettede.

Loop hvor brugerne sidder med hovedet nedad
Hvor er kraften som modsvarer den kraft, vi kan føle når karussellen drejer rundt? Den findes ikke, fordi vi ikke er i et inertialsystem. Beregner man kraften, man kan føle i det roterende koordinatsystem, får man udtrykket m a = m rω 2, som er det samme udtryk som før, men hvor kraften, centrifugalkraften, peger udad. Hvis man sidder i en rutsjebane og kører ned i et loop, er det centrifugalkraften, man føler trykker en ned i sædet – omvendt mærker man en reaktionskraft fra sædet, der sørger for, at man ikke falder ud gennem bunden af vognen. En iagttager, der ser på turen fra tivoliet, vil sige, at der virker den centripetalkraft på dig, som er nødvendig for at give en cirkelbevægelse, og den holder dig i sædet. Tager man en elektronisk kraftmåler i lommen, medens man er i vognen, vil den vise en kraft ”udad” (nedad imod vognens bund).
Koordinatsystemer
I eksemplet ovenfor med karrusellen ses bevægelsen ud fra to forskellige koordinatsystemer: I det faste system udfører legemet en cirkelbevægelse, og den nødvendige centripetalkraft leveres af gnidningsmodstanden mellem klods og underlag.

Centrifuge til at opnå mange "g" på personer
I det roterende system prøver centrifugalkraften at slynge legemet ud og legemet fastholdes af gnidningsmodstanden (centripetalkraften), altså to lige store kræfter, modsat rettede, som ophæver hinanden, så den betragtede masse ligger stille på karrusellen. Centrifugalkraften eksisterer således kun i det roterende koordinatsystem, og er i denne forstand en kraft man ”føler”. Havde vi set på kræfterne i et fysisk system fra to forskellige inertialsystemer, havde sagen været simplere. Sådanne to systemer kan findes, for hvis vi har ét inertialsystem, kræver det kun, at det andet bevæger sig med konstant hastighed (størrelse og retning), i forhold til det vi har. Så er begge inertialsystemer. I det tilfælde gælder identiske newtonske love i de to systemer
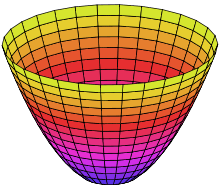
Væskeoverfladens form i en centrifuge
Accelererede koordinatsystemer
Fiktive kræfter dvs. kræfter tilsyneladende uden oprindelsesgrund, optræder i alle accelererede koordinatsystemer, som f.eks. roterende systemer. Et langt simplere eksempel er følgende: Hvis man stiller sig på en badevægt (med fjeder) i en elevator, vil man se, at den viser mere når elevatoren starter (accelererer) opad, og mindre når den starter og accelererer nedad. Det er ikke symptom på, at man har fået større eller mindre masse (der er ingen lette veje til afmagringskure). Det skyldes, at elevatoren ikke er et inertialsystem, medens den accelererer. Det er den imidlertid ved konstant hastighed. Så snart den kører med konstant hastighed, er vægtens visning normal. Det er altså principielt helt samme type af effekt. Tilsvarende bliver man trykket tilbage i sædet i en accelererende bil og slynget frem når den bremser eller rammer noget.

Kunstig tyngdekraft i fremtidens roterende rumstation (A Clarck/S Kubrick)
Med venlig hilsen
Finn Berg Rasmussen
Malte Olsen
