Giver rørforstærkere bedre lyd end transistorer?
Ved forstærkning af lyd fra eksempelvis en elguitar er der nogle der mener, at der er bedre og mere "varm" lyd fra en rørforstærker end fra en transistor-forstærker.
Er der ikke tale om bias? Umiddelbart kan jeg ikke se ud fra fysikken, at der skulle være en forskel, udover at lyden kan behandles elektronisk og med software i nymodens forstærkere.
Venlig hilsen
Jens Paaby
Pensioneret læge

Svar:
Hej Jens,
Jeg er enig i, at der er stor risiko for et nostalgisk bias i stil med at foretrække vinylplader from for .mp3-filer. Så en (muligvis dominerende) effekt skal måske findes i psykologien.
Skal jeg alligevel prøve at give en fysisk årsag til, at der kunne være en reel effekt, så bliver det følgende:
Hvad er en forstærker?
En forstærker virker grundlæggende ved at have et relativt kraftigt spændingsfald, som kan accelerere ladede partikler henover et et lille "hul" i et kredsløb, så kredsløbet sluttes, men hvor der så indsættes en lille spændings-"bump", som forhindrer ladningerne i at passere.
Et svagt signal (f.eks. fra en guitar) kan så "sænke" og "hæve" dette bump, så ladninger kan passere / ikke passere, og skabe et stærkt signal, som ledes ud til højttaleren.
Gammeldags rørforstærkere består af et metalgitter placeret mellem to metalplader, og guitarens (svage) signal kan så ændre spændingen i gitteret og tillade en (kraftig) strøm at løbe mellem pladerne. For at strømmen kan løbe, kræves dog et vakuum, så derfor placeres de i glasrør, som suges tomme for luft.
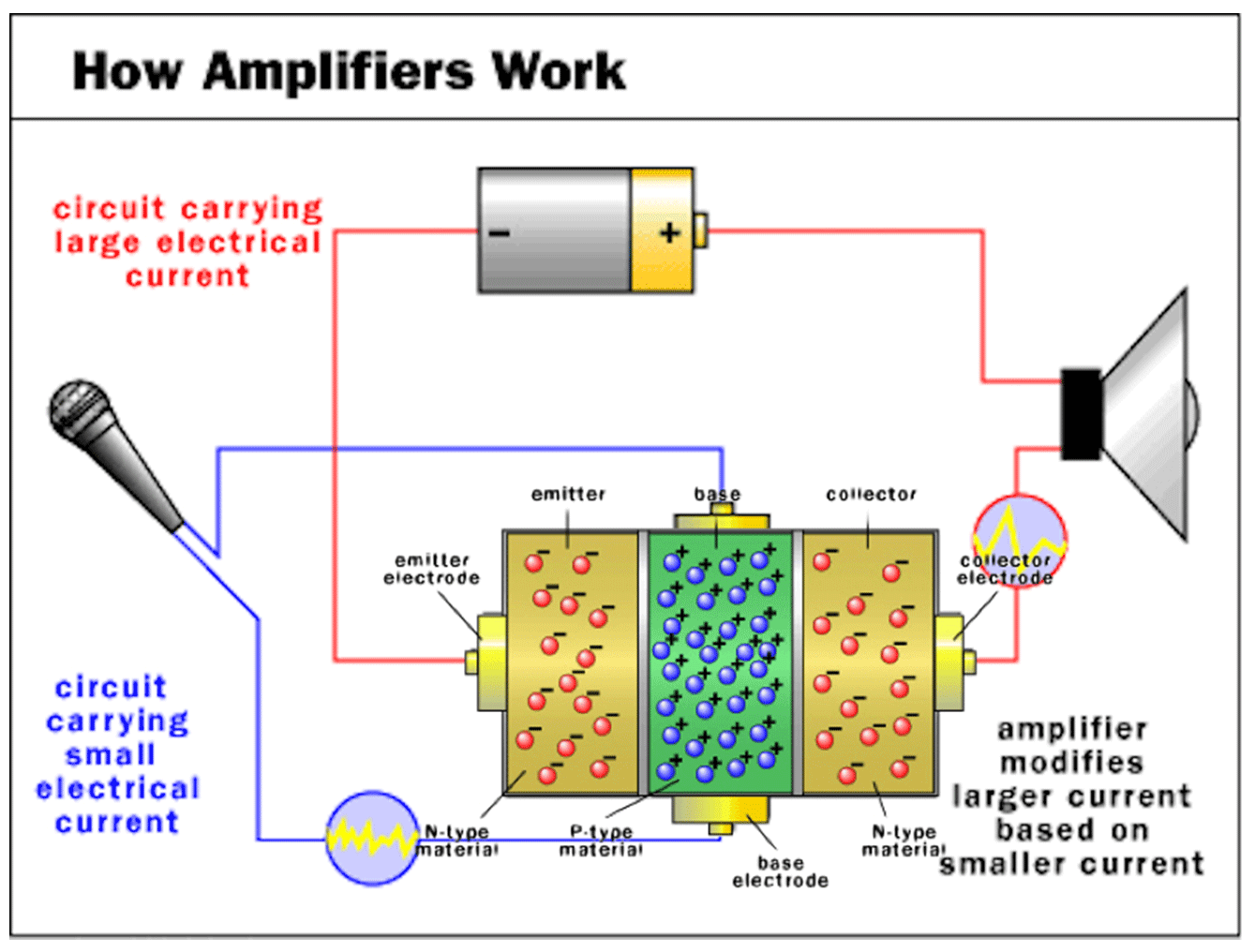
Princippet bag en forstærker. Kilde: Circuits of Today.
I 1948 kom så transistoren, som i begyndelsen var omtrent lige så stor, men med årene er blevet udviklet til at være en milliard gange mindre.
Her er ideen, at vakuummet erstattes af et halvleder-materiale, og det svage signal kan så ændre spændingsbumpet ved at donere flere eller færre elektroner til halvlederen.
Fra svagt til stærkt signal
I begge tilfælde kan man beskrive den måde, som det svage signal resulterer i det stærke signal, med en matematisk funktion. Det svage signal kan f.eks. være en ren sinus-bølge, som ændrer sig med tiden t på følgende måde:
![]() Her er ω frekvensen, og A er amplituden, dvs. hvor kraftigt signalet er. Det er altså A vi gerne vil prøve at gøre kraftigere, og forstærkeren kan så beskrives matematisk ved en anden funktion, som vi kan kalde f(x).
Her er ω frekvensen, og A er amplituden, dvs. hvor kraftigt signalet er. Det er altså A vi gerne vil prøve at gøre kraftigere, og forstærkeren kan så beskrives matematisk ved en anden funktion, som vi kan kalde f(x).
Et signal som det ovenstående x(t) svarer til en "ren" tone fra f.eks. et keyboard. Et instrument som f.eks. en guitar har mere komplicerede signaler, selv hvis du bare picker en enkelt streng, fordi der skabes en masse "overtoner" af strengen selv, af de andre strenge, og af guitarens krop.
Det er forholdet mellem disse overtoner, der gør, at du kan høre forskel på f.eks. tonen B (som på engelsk kaldes B♭) på 466 Hz fra en guitar, en trompet, og et menneske.
For både rørforstærkere og transistorer er det en ingeniørmæssig kunst at udvikle dem sådan at den matematiske funktion f(x) ikke ændrer input-signalet x(t) for meget (med mindre man ligefrem er interesseret i at ændre det, som f.eks. med effekter som distortion, overdrive, chorus, og hvad der eller findes).
Uanset hvordan vi konstruerer forstærkeren, kan vi beskrive funktion sådan her:
![]()
hvor α, β, γ, δ, ε, ζ, … er konstanter. Altså, en i princippet uendelig sum af input-signalet opløftet til forskellige potenser, og ganget med forskellige konstanter.
Hvis alle andre konstanter end α er nul, er forstærkningen blot f(x) = αx. En sådan forstærker tager altså input-signalet x og ganger det med et konstant tal, og hvis denne konstant er et stort tal, forstærker vi signalet meget.
Dette en en "lineær" forstærker, på den måde at input og output er fuldstændig ens, bortset fra lydstyrken.
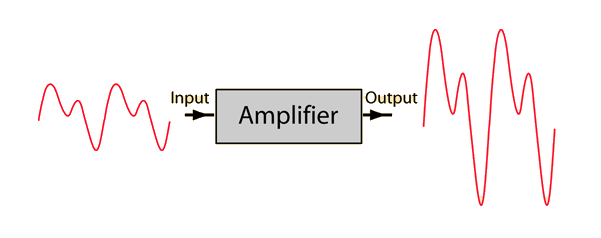
Forskellen på rørforstærkere og transistorer
Sådan en ideel forstærker er dog ikke mulig i virkeligheden. Der er rigtig mange faktorer, der spiller ind og påvirker outputtet, så de andre konstanter vil have værdier, som er større end nul. Hvis f.eks. konstant #2, altså β, er stor, fås et væsentligt bidrag fra x², altså input-signalet i anden potens, dvs. (sin ωt)².
Man kan vise matematisk, at denne faktor, (sin ωt)², er lig med ½ + ½cos 2ωt. Og hvad betyder dét så?
Jo, det betyder, at outputtet forstærkes med en konstant (½), hvilket er fint, men også med den dobbelte frekvens, fordi der står et 2-tal foran frekvensen ω. Dobbelt frekvens betyder "en oktav højere", så outputtet vil altså have en "falsk", lysere tone.
Jeg skrive falsk i gåseøjne, fordi den ikke kommer fra instrumentet, men det lyder ikke falsk, for det er stadig den samme tone, bare lysere (det er så også et cosinus-signal i stedet for et sinus-signal, hvilket er det samme bortset fra en faseforskydning; dette kan måske alligevel høres).
Og nu kommer vi endelig til svaret:
Det viser sig, at rørforstærkere har en tendens til at skabe forstærkning hvor alle konstanterne foran led med x opløftet til lige potenser er relativt høje (altså α, γ, ε, …), mens konstanterne foran de tal med ulige potenser undertrykkes (altså β, δ, ζ, …). Effekten af dette er, at lyden forstærkes, og at der godt nok kommer en masse "falske" toner, men disse toner passer stadig sammen med de originale toner, fordi det blot er et helt antal oktaver højere. De harmonerer.
I modsætning hertil, viser det sig, kan transistorer have en tendens til signifikante værdier for konstanterne ud for de ulige potenser af x. Nogle af disse led kan give overtoner som tertser og kvinter, og det gør ofte ikke så meget. Kender du lidt til musik, ved du måske, at dette f.eks. er tonerne hhv. H (eng.: B) og D, hvis grundtonen er G, og disse toner er allerede i en G-dur-akkord.
Men nogle af leddene kan give overtoner, som dissonerer med input-tonen. Og f.eks. er B ikke godt at have med i en G-dur-akkord, da B hører til en G-mol. Det lyder frygteligt. Lyt selv her:
Så: Rørforstærkere kan måske tænkes at give en "renere" eller "varmere" lyd end transistorer.
Men… forudindtagethed spiller nok også en rolle :)
Bedste hilsener,
Peter Laursen, Astrofysiker og videnskabsformidler
Cosmic Dawn Center, Niels Bohr Institutet.

