Hvordan kan en glaskugle hoppe mere end en bold?
Hej Spørg om Fysik
Min datter har en masse af de velkendte, klassiske glaskugler, og det undrer mig rigtigt meget, at når hun taber dem på vores stengulv, så hopper de mere end hoppebolde. Kuglerne er jo lavet af massivt glas, og bestemt ikke elastiske - så hvordan kan det være?
Tusind tak for muligheden for at spørge jer til råds.
Med venlig hilsen
D H

Når to legemer støder sammen, afhænger resultatet såvel af det materiale legemerne er fremstillet af, såvel som den hastighed de har ved sammenstødet.
Tager man to stålkugler og lader dem støde sammen, vil de hoppe tilbage fra hinanden næsten med samme fart, som de havde lige før de ramte hinanden. Tager man to bløde ler-kugler med samme masse som stålkuglerne, og lader dem støde sammen med tilsvarende hastigheder, vil de flades ud og hænge sammen til et legeme efter sammenstødet.

Den såkaldte Newtons vugge
Desuden giver man stålkuglerne fart nok, vil de før eller senere gå i stykker eller i det mindste få skader, så de ikke er runde mere. , hvis overfladen brydes. Hvis man to ens stål og glaskugler og lod dem falde fra større og større højde, ville glaskuglen splintres på et eller andet tidspunkt før stålkuglen tog skade, og gå i stumper. Det gælder alle materialer. Det sker som regel ved en meget mindre hastighed for glaskuglerne. I øvrigt er glas set fra et fysiksynspunkt ikke et fast stof, men en meget tyktflydende underafkølet væske. Ser man på ruderne i århundrede gamle huse, kan man se at vinduerne er blevet tykkere forneden, vinduets glas løber ganske langsomt nedad.
Man kan tydeligt selv føle elasticiteten i stål, ved at slå slagfladerne på 2 nogenlunde ens hamre imod hinanden, og bagefter sammenligne ved at slå med en hammer på f.eks. et stykke ler, bly eller en stor kartoffel.

Projektiler efter stød
Fysikerne beskriver sammenstød imellem genstande, stød, ved hjælp af impulssætningen. Den siger at summen af masse gange hastighed (altså med retning) af det ene legeme før stødet og det andet legeme før stødet skal, være identiske med summen af masser gange hastigheder efter stødet.
m1*v1 + m2*v2 = m1*u1 + m2*u2
hvor m1 og m2 henviser til de to legemers masser, v til hastigheder før stødet og u til hastigheder efter stødet. I tilfælde af at kuglerne hænger sammen efter stødet som lerkuglerne ovenfor, bliver højresiden i stedet ændret til
m1*v1 + m2*v2 = (m1 + m2)*u.
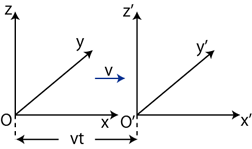
De bevægede koordinatakser
Man er derfor nødt til at inddele stødene i flere modeller, idet der kan være energibevarelse ved et stød, som det stort set er ved stålkuglerne, eller der kan være energitab som ved lerkuglerne. I lerkuglestødet er der altså tab, noget af energien bliver brugt til at opvarme leret lidt. I praksis er der næsten altid i det mindste små tab. En bold man lader falde til jorden, kommer ikke helt så højt op som startstedet uanset materialet.
Som stød hvor der sker deformation af det stødende legeme, vil de fleste have set projektilet fra et luftgevær, der har ramt et stykke jern eller træ og blevet klemt helt flad.
Den anden faktor som indgår i forsøget er de elastiske egenskaber
De elastiske egenskaber indgår også når der sker en deformation, men når det ikke sker, er det de elastiske egenskaber der bestemmer hvor nær energibevarelse stødet er. En superbold har gode elastiske egenskaber, der sker kun meget lidt energitab i stødet. Det samme gælder en stålkugle, og altså også glaskugler. Glas er et glimrende elastisk stof indtil en vis grænse, derefter går det i stykker, som vi alle ved af erfaring. Man kan købe hærdede drikkeglas, som faktisk kan hoppe ganske pænt på et stengulv, men som går i næsten pulverformige stykker. Hvis man kommer i nærheden af store 6 eller 8 mm vinduer kan man let se, at de virker som elastiseketrommeskind, hvis man giver dem et let slag med hånden, altså glas er elastisk. Glas af særlige typer kan være op til 8 gange mere elastisk end rustfrit stål.

Hoppende bold fotograferet i stroboskoplys
Man kender i øvrigt glas elasticitet fra glasfiberarmerede plastmaterialer, såsom f.eks. møllevinger, ketchere, buer til pileskydning, golfkølleskafter, bådskrog osv. Her giver glas samtidigt stor brudstyrke og elasticitet, samt ringe vægt i forhold til de fleste andre materialer - noget der netop er behov for til disse formål. Glas er på disse steder man mange gange i dag ved at blive udskiftet med kulfibre, som er endnu bedre til flere af formålene.
Komplet elastiske bolde, dvs. bolde som ikke har energitab ved stød, findes ikke. Man kan komme ret nær med de bedste materialer, f.eks. superbolde, kuglelejekugler osv. men der er tab, og kuglen af materialet holder efterhånden op med at hoppe.
Med venlig hilsen
Malte Olsen
