E = mc²: Hvorfor har lys energi?

Svar:

Dit spørgsmål omhandler i virkeligheden to forhold, nemlig "Hvorfor har fotoner energi?" og "Hvad sker der med E, når m = 0?". Lad os tage det sidste først:

Svaret er, at »E = mc²« kun er den halve sandhed af den ligning, du måske kender som "Einsteins ligning".

Den hele sandhed er, at den totale energi E, som en partikel (eller flere partikler tilsammen) har, også afhænger af deres såkaldte impuls (som i gamle dage blev kaldt "bevægelsesmængde", og på engelsk hedder "momentum").

For at forstå det bedre, må vi bruge en lille smule matematik, men det bliver ikke sværere end en kvadratrod, og jeg skal nok forklare hvad de enkelte ligninger betyder på ikke-matematisk.

(Svaret blev lidt langt; hvis du er utålmodig, kan du skippe til konklusionen.)

Impuls

Hvis du har lært om impuls i gymnasiet, så fik du nok at vide, at en partikel med massen m har impulsen p = mv, hvor v er hastigheden. Altså, jo større masse og jo større hastighed, jo større impuls.

Men relativitetsteorien modificerede dette en smule ved at gange en faktor på, som kaldes "Lorentz-faktoren", og som skrives med det græske bogstav gamma, γ. Altså, p = γmv. Denne faktor er

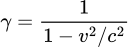hvor c er lysets fart. 

Du kan se, at når v er tæt på nul, så er v²/c² meget tæt på nul, og derfor bliver Lorentz-faktoren meget tæt på 1, og kan derfor ignoreres. Det betyder, at ved normale hverdagshastigheder, så er "p = mv" en utrolig god approksimation.

Du kan også se, at jo tættere v kommer på c, jo tættere kommer v²/c² på 1. Så står der "én minus noget der er tæt på én" nede i brøkens nævner, og derfor bliver γ større og større, uden grænse. Men idet en partikel med masse aldrig kan komme helt op på v = c, så bliver γ aldrig helt uendelig stor. Man kan også udtrykke det som "Det ville kræve uendelig meget energi at accelerere en partikel op til lysets fart".

Energi-impuls-ligningen

Den ligning, som du og det meste af verden kender, er en speciel udgave af en lidt længere ligning, som formelt kaldes "energi-impuls-ligningen", og som man med lidt algebra og kalkulus kan vise er:

E  =  (pc)² + (mc²)²

Lad os prøve at se på, hvad denne ligning fortæller os i nogle særlige tilfælde:

Tilfælde 1: ingen bevægelse

Hvis en partikel ligger stille, så er v = 0, og derfor er p og dermed (pc)² også 0. Tilbage står så bare E² = (mc²)², eller E = mc². Denne "populære version" af Einsteins ligning fortæller altså, hvad partiklens energi er, når den ligger stille. Selve partiklens masse bidrager altså til dens energi. Somme tider kalder vi også denne masse for partiklens "hvilemasse", fordi man godt kan tolke ligningen som at massen stiger, hvis den ikke er i hvile. Denne fortolkning er dog uddateret

Tilfælde 2: langsom bevægelse

Hvis en partikel bevæger sig langsomt (ift. lyset), så kan man (vha. af et smart matematisk trick, som hedder Taylor-ekspansion) omskrive energi-impuls-ligningen til at sige E ≈ mc² + ½mv². Hvad denne approksimative version siger er, at partiklen har sin "masse-energi" (mc²), som ikke ændrer sig uanset hvad partiklen foretager sig, plus noget ekstra energi fra dens bevægelse (½mv²). Dette er partiklens kinetiske energi, eller "bevægelsesenergi", som du lærte i folkeskolen.

I almindelig, "klassisk" mekanik beskæftiger man sig sjældent med legemers absolutte energi, men oftest mest forskelle i energi, f.eks. når en sten falder fra en vis højde, og dens potentielle energi omdannes til kinetisk. Fordi "mc²"-leddet ikke ændrer, behøver man slet ikke tage det med i sådan nogle beregninger, og derfor lærte du at E = ½mv².

Tilfælde 3: hurtig bevægelse

Hvis en partikel ikke har nogen hvilemasse, så kan den ikke ligge stille, men er dømt til at bevæge sig med lysets fart. Udover fotoner gælder dette gluoner (som overfører den stærke kernekraft) og gravitoner (som er en hypotetisk partikel, der, hvis den eksisterer, overfører tyngdekraften). I dette tilfælde er energi-impuls-ligningens sidste led (mc²)² = 0. Tilbage står så E² = (pc)², eller blot E = pc.

Denne version fortæller os, at masseløse partikler som f.eks. fotoner faktisk har impuls! Lige om lidt ser vi på, hvorfor fotonen overhovedet har energi, men denne version af energi-impuls-ligningen siger altså, at en foton med energien E har impulsen p = E/c.

Det betyder, at fotoner er i stand til at "skubbe" til ting. Når en foton rammer noget, overfører den sin impuls til det den rammer, og udøver dermed et tryk. Sådan en foton er jo en bette fætter, men er der nok af dem, og er dét de rammer let nok, kan det alligevel give en effekt.

Dette udnytter man i solsejl, som er kæmpestore, men ekstremt lette, sejl på visse satellitter, som kan fange Solens lys og derved langsomt, men ganske gratis, kan accelerere. Der er endda planer om rumsonder, som skal kunne accelereres vha. kraftige lasere, som kan opereres fra Jorden.

Hvor kommer fotonens energi fra?

Einsteins ligning fortæller os altså ikke, at fotonernes energi er 0. Men hvor kommer deres energi egentlig fra?

Fotoner er svingninger, eller bølger, i det elektromagnetiske felt, som udbreder sig med lysets fart. Ligesom med alle andre former for bølger og svingninger, har fotoner mere energi, jo hurtigere de svinger, dvs. jo højere deres frekvens er.

Frekvensen betegnes med det græske bogstav "ny" (ν), og fotonernes energi er så givet ved ligningen E = hν, hvor h er et meget, meget lille tal, der hedder Plancks konstant, og som ofte optræder ifm. kvantemekaniske beregninger.

Fotonerne bliver altså skabt med deres energi, og den proces der skaber dem, bestemmer hvor meget. Hvis en foton udsendes fra et atom ved at en elektron falder fra en tilstand med høj energi til lav energi, er fotonens energi lig med forskellen i tilstandenes energier. Og Einsteins ligning fortæller os så, at atomet efter udsendelsen vejer en lille smule mindre, nemlig E/c².

Hvis fotonen udsendes fordi en partikel har mødt sin onde fætter, dens anti-partikel, ophører begge med at eksistere, og bliver i stedet til to fotoner hvis samlede energi er partiklernes samlede masse gange c² (plus eventuel kinetisk energi, som partiklerne havde før de mødtes, adderet som beskrevet ved Einsteins ligning).

Jo hurtigere en foton svinger, jo kortere bliver dens bølgelængde, og alt efter hvilken frekvens/energi/bølgelængde de har, kan fotoner have forskellige egenskaber. Ligger deres bølgelængde f.eks. mellem ca. 400 og 700 nanometer, kan vi se dem med vores øjne, er de 100.000 gange længere kan vi bruge dem til at varme vores kylling op i mikroovnen, og er de 10.000 gange kortere, kan vi bruge dem til at tage billeder af vores knogler.

Konklusion

Så for at opsummere: Fotonerne har energi, og dermed impuls, fra den proces der har skabt dem. Så selv om deres hvilemasse ganske rigtigt er 0, giver Einsteins ligning ikke 0 for deres energi, fordi den fulde ligning også inkluderer impuls.

Bedste hilsener,
Peter Laursen, Astrofysiker og videnskabsformidler
Cosmic Dawn Center, Niels Bohr Institutet.