Tunnel igennem jorden

Hej Spørg om Fysik
Jeg har et avanceret spørgsmål om jordens tyngdekraft, som jeg håber i kan guide videre til en kyndig person som kan hjælpe mig.

Spørgsmålet er som følger:

I forbindelse med at jeg har lavet et forløb om avanceret matematik med nogle meget dygtige elever, havde en elev set et program på Discovery Channel, som omhandlede teorien om, at man kunne bygge en tunnel gennem jordens indre, som derved fungerede som en elevator, der blev trukket ned af tyngdekraften, og derefter igen blev bremset af tyngdekraften.

Vi gav os til at beregne på rejsetiden gennem jorden i en sådan tunnel, hvor jeg forudsatte at tyngdekraften gennem jorden konstant ville være 9,81 m/s². Ved nærmere eftertanke vil jeg mene, at tyngdekraften gennem jorden næppe er konstant, men i starten må stige i takt med at man nærmer sig kernen som har en højere massefylde, mens den til sidst vil falde mens vi nærmer os selve kernen, og helt i midten må den være 0 m/s².

Er min antagelse rigtig, og er det muligt at estimere tyngdekraftens ændring på rejse gennem jorden?

Det lille billede på forrige side viser verdens dybeste mineskakt Western Deep Levels Mine, Transvaal i Sydafrika 3582 m dyb

Mange hilsener
J J

For at forstå tyngdekraften inde i jorden må vi først forestille os jorden som en kugleflade af passende tykkelse og ens masse pr kvadratmeter (altså en hul jord formet som en bold).

Figuren (fra L. Hogben: Videnskab for hvermand) viser den hule jord med en mand anbragt et tilfældigt sted imellem New York (NY) og Cape Town (CT). Afstanden til Cape Town er, r, til New York R.

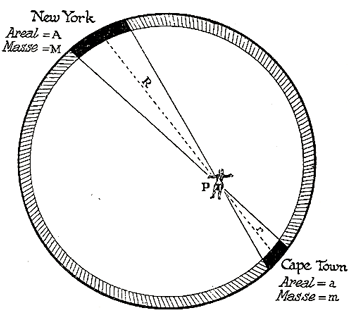De mørke arealer som afskæres af de viste kegler har et areal der er proportionalt med afstanden i anden, dvs. kaldes massen af overfladen i NY for A og massen af overfladen i CT for a fås:

M:m = R² : r² .

Newtons gravitationslov siger, at kraften fra en masse kan skrives F = G.( M * m)/x^{2 ,} hvor x er afstanden imellem legemernes tyngdepunkter, M og m masserne F kraften og G den universelle gravitationskonstant. Herfra får man for tiltrækningen fra de to overfladestykker i NY og CT:

G*M/R² = G*m/r²

Det ses, at tiltrækningskraften fra NY præcis er lige så stor som tiltrækningskraften fra CT. Det vil gælde uanset hvilke parvise kegler, vi ser på så indeni, i den hule kugles vil massen fra overfladerne præcis ophæve hinanden parvist. Hvis man altså går ned i jorden kommer tyngdekraften (og dermed tyngde­accele­rationen), kun fra den del af jordkuglen, der har radius mindre end svarende til det sted, man er. Det der ligger udenfor ophæves af det tilsvarende bidrag fra modsatte side. Da rumfanget af en kugle er V = 4/3 *π*R³, hvor R er radius til det sted man er. Massen af den del af jorden er M  =  4/3 *π*R³ *ρ, hvor ρ er densiteten af jorden (i middel ρ = 5,518 *10³ kg/m³). Det betyder, at man for tyngdekraften får F = G M*m/R² = G* (4/3 *π*R³ *ρ  * m)/R² = konstant *R, så den aftager proportionalt med R og er nul i centrum. Ud fra kendskabet til jordens sammensætning, densiteter og radier for de forskellige densiteter er det altså muligt nogenlunde at udregne tyngdeaccelerationen i alle afstande fra centrum og dermed farten og tiden for faldet tværs igennem jorden.

Virkeligheden er mere kompliceret fordi der er stenarter nær overfladen og jern-nikkel i de centrale del af jorden så der er ikke tale om nogen kontinuert overgang.

Når I skal til at lave hullet er der nogen der har påbegyndt det for jer. I Kimberley the big hole ca. 50 000 minearbejdere gravede det med hakke og skovl det gav 2720 kg diamanter, 463 m bredt, og 240 m dybt, se foto. Den dybeste mine i verden er så vidt jeg kan opspore også i Sydafrika. Det er Western Deep Levels Mine, Transvaal i Sydafrika 3582 m dyb, vægtemperatur ved bunden 55 ⁰C. Der er altså i alle tilfælde en del arbejde tilbage for at lave et hul hele vejen igennem.

Bevægelsen igennem jorden kan i øvrigt ses som projektion af den cirkelbevægelse en satellit vil have i jordoverfladehøjde (hvis det kunne lade sig gøre). Omløbstiden kan fås ved at skrive centripetalkraften som F = mg, fra cirkelbevægelsen fås den samme kraft som F = m R ω² med  ω = 2 π/T, hvor T er omløbstiden fås T = 5059 sek. = 84,32 min og hastigheden i centrum V = 7,9 km/s = 28 500 km/h. Turen igennem jorden vil altså tage det halve af omløbstiden.

Med venlig hilsen
Malte Olsen