Ændres lysets hastighed?
Hej Spørg om Fysik
Jeg skriver på baggrund af en diskussion i vores fysiktime på gymnasiet. Jeg stillede i en time et spørgsmål, der gik på hvordan det kan lade sig gøre, at elektromagnetisk stråling kan passere med én hastighed v1 gennem et medie, f.eks. glas, da have en hastighed v2 < v1, og efter at have rejst gennem mediet igen have en hastighed v = v1?
Ovenstående bygger på at vi ved, at lyset (e.magn. stråling) har én værdi c i et givent medium. I vakuum c = 299.799,458 km/s. I glas er hastigheden dog mindre, men når lyset så igen når ud i vakuumet på den anden side af glasset, så vil hastigheden jo være nødt til at være c = 299.799,458 km/s igen? Hvordan kan dette være?
Det lyder næsten som om, at lyset bærer en eller anden form for bevaret indre energi, der gør det i stand til at "accelerere" i overgangen mellem glas og vakuum?
Eller har vi fuldstændig misforstået noget?
Med venlig hilsen
TLT

For elektromagnetiske bølger gælder at λ*f = c, hvor λ er bølgelængden af bølgen, f frekvensen og c lyshastigheden i det medium, hvor strålingen breder sig. Om energiindholdet i lyset gælder, at E = h*f, hvor h er Plancks konstant og E energien.

Mindeplade for Max Planck opsat på Humboldt Universitetet i Berlin. På dansk lyder teksten: "Max Planck, opdageren af virkningskvantet h, underviste i dette hus fra 1889 til 1928."
Kilde: Wikipedia
Da der skal være energibevarelse ved overgang fra et medie til et andet må frekvensen, f, altså være det der er bevaret (er konstant) ved overgangen. Når vi taler om forskellige medier, er medierne her karakteriseret ved lyshastigheden, c, i mediet (eller vakuum). Ved overgang fra et stof til et andet ændres altså hastigheden samt bølgelængden, men energien bevares. Du har altså ret i den henseende, at der er en energibevarelse.
Ser man tilsvarende på lydbølger så er den laveste tone på et klaver (A0) 27,5 Hz, strengens længde kan være ca. 1,5 m (½ bølgelængde). Den svinger og sætter luften i svingninger og laver en tone der har en bølgelængde i luft på ca. 12 m. Hastigheden går fra ca. 80 m/s til 330 m/s noget afhængigt af temperaturen. Overførselen sker ved at strengens tværgående bevægelser rammer luftmolekylerne og skiftevis skaber kompression og ekspansion.
Molekylerne i nærheden af strengen har altså i middel præcis samme hastighed som strengen. Vil man opfatte resultatet som en acceleration af bølgen, næppe, kun overførsel af partikelbevægelsen.
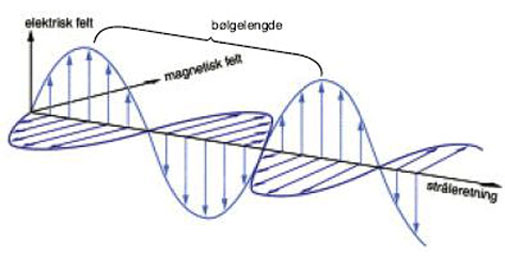
Elektromagnetiske bølger
Når det drejer sig om lys sker udbredelsen som svingende elektriske og magnetiske felter (normalt vinkelret på hinanden). Der er ikke nogen genstand, som skal have en acceleration, felterne skal bare opfylde Maxwells ligninger, den korte model af resultatet for simple stoffer er bølgeligningen her øverst. Der er altså ikke i denne forstand nogen træghed (inerti), der skal overvindes, eller noget der skal accelereres. Det er felternes udstrækning der bestemmes af stofkonstanterne (lyshastigheden) og frekvensen helt svarende til udbredelsen af toner.

James Clerk Maxwell (1831 - 1879)
Man kan på den anden side anskue problemet sådan: Lys er jo elektromagnetiske bølger, der opfylder Maxwell's berømte ligninger. Før bølgeforklaringen blev etableret, legede Newton med tanken om, at lys består af partikler, og kunne fx forklare, at en lysstråle afbøjes, når den går fra et materiale til et andet, fx fra luft til glas.
Siden har vi jo fundet, at ifølge kvanteteorien så beskrives selv partiklers bevægelse med en bølgeligning. Hvis man nu opfatter Maxwells ligninger, som de kvantemekaniske ligninger for lyspartikler, så går det hele op i en højere enhed: Lyspartiklerne vil opfatte området med glas, som et område med lavere potentiel energi, og deres hastighed vil øges. Det er som om det går stejlt ned ad bakke for lyspartiklerne, lige når de bevæger sig fra luft til glas. Omvendt går det så op ad bakke når de sidenhen forlades glasset. Kvanteteorien har i en vis forstand givet Newton delvis ret i sin beskrivelse af lys.
Med venlig hilsen
Per Hedegård
Malte Olsen
