Opvarmning af et materiale foran en pære

SVAR:

Hej Jesper,
Det er et temmelig komplekst spørgsmål du stiller, som en ingeniør nok vil være bedre rustet til at besvare end en fysiker, men jeg kan give dig nogle generelle betragtninger: 

Lampens effekt

LED-spotlamper har typisk en effekt P på måske 3–15 W. Lad os for eksemplets skyld tage P = 10 W. Omkring 75–80% af energien kommer ud som lys, mens resten går til at varme lampen op. LED-lamper bliver ikke så varme som glødelamper (hvilket er grunden til, at de er smarte, da glødelamperne har et langt større tab til varme isf. lys). Denne andel kaldes "lys-effektiviteten" og benævnes somme tider med et V. Hvis V = 0.8, betyder det altså, at en 10 W-pære udsender ca. 8 W som lys, altså 8 Joule i sekundet.

Hvor varme LED-pærer bliver afhænger af designet, men 80 °C er nok ikke helt ved siden af.

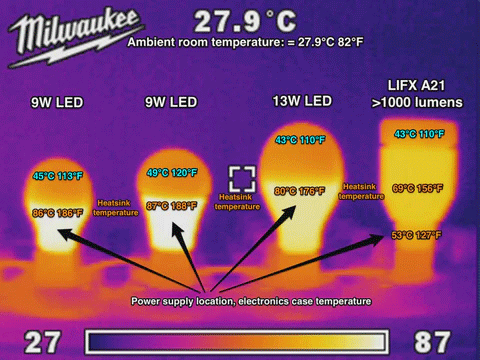
Temperaturen af forskellige LED-pærer. Kilde: LIFX.

Absorption af stråling

Et materiale har en vis albedo, A, eller "refleksionsevne", som er et tal mellem 0 og 100%. Et stykke hvidt papir har måske 90%, mens sort papir har ~10%, og et stykke bølgepap har en albedo et sted midt imellem.

Lad os sige, at du tager et stykke pap med en albedo på 30%, dvs. A = 0.3. Pappet reflekterer altså 30% af det indkommende lys, mens 70% absorberes, varmer pappet op, og udsendes som varmestråling, dvs. infrarødt lys.

Hvis du holder pappet helt op til LED-pæren, vil de reflekterede 30% dog komme ind i lampen igen. Hvis lampen har et reflekterende coating på bagsiden, vil lyset blive sendt tilbage til pappet, som igen vil absorbere noget, og reflektere noget, osv.. Resultatet er, at pappet effektivt set vil absorbere det meste af lyset, altså A ~ 0. Lad os for eksemplets skyld sige A = 0.1.

Opvarmning

Hvor meget et materiale varmes op, dT, når det modtager noget varmeenergi, dQ, afhænger af dets (specifikke) varmekapacitet, c = dQ/m dT, hvor m er materialets masse. Pap og papir har en varmekapacitet omkring c ~ 1,3 J/g/°C. Det betyder, at du skal putte 1,3 Joule ind i 1 gram pap, for at få dets temperatur T til at stige 1 grad.

Hvis du holder papper helt op til pæren, lander al strålingen på et lille område. Hvis f.eks. pæren er sådan en lille rund én man sætter op i loftet på badeværelset, lander lyset måske på et 25 cm² stort område.

Overfladetætheden af pap er måske 1 kg/m², eller 0,1 g/cm² (hvis det er under 600 g/m² kaldes det karton). Et stykke pap på 25 cm² vejer dermed m = 2,5 g. Pappets temperatur stiger derfor med

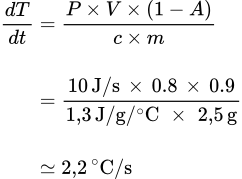eller godt 2 grader i sekundet.

Termodynamisk ligevægt

Denne temperaturstigning gælder i starten af dit eksperiment, men kan ikke blive ved, af to årsager:

For det første bliver energien ikke inde i dine 25 cm² pap. Energi kan mistes på tre måder, kaldet emission, konvektion og konduktion. Noget af det udsendes som nævnt ovenfor som infrarød stråling, noget af det overføres til den omkringliggende luft, og noget af det diffunderer ud til resten af papstykket.

Generelt stiger energioverførslen mellem to objekter med temperaturforskellen mellem de to objekter. Jo varmere papstykket bliver, jo hurtigere mister det varme, og derfor varmes det hurtigt op i starten, men efterhånden vil temperaturstigningen gå langsommere og langsommere. Resultatet vil være en omtrent eksponentielt aftagende effektivitet, sådan at temperaturen stiger med tiden nogenlunde proportionalt med en faktor (1 – e^{–[konstant]⨉[tid]}).

Hvis pappet kun udstrålede energien, ville vi kunne bruge Stefan–Boltzmanns lov, som siger at den udstrålede energi er proportional med temperaturen i fjerde potens, og at den udstrålede energi pr. tid er

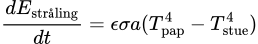hvor ε er emissiviteten, som vi kan sætte til 0.95, σ = 5.67 × 10^–8 W/m²/K⁴ er en konstant, og a er arealet af pappet. Hvis vi antager, at pappets varmeledningsevne er så høj, at temperaturen er den samme på for- og bagside, er arealet så a = 50 cm².

Konvektion giver dog også et bidrag:

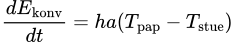
Her er h en "konvektionskoefficient", som ikke er lige til at bestemme. Jeg har konfereret lektor emeritus Lars Øgendahl, som fortæller mig, at "Der findes alle mulige beregninger og simuleringer af størrelsen af denne hvori der indgår alle mulige dimensionsløse skaleringsparametre, Reynolds tal, Nusselt-tallet, Prandtl-tallet og Grashof-tallet.

Disse afhænger af luftens viskositet, densitet, varmekapacitet og varmeledningsevne samt temperaturforskellen til omgivelserne (!) og form og størrelse på det objekt, der afgiver/modtager varme via konvektion. Ubehageligt!"

Hvis man slår de to mekanismer sammen og antager at pappets temperatur T_pap ikke er for langt fra stuetemperaturen T_stue, kan man linearisere summen:

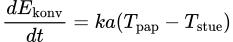hvor k er en ny konstant.

Lars har endda været så flink at løse denne differentialligning, og resultatet bliver, at temperaturen T stiger med tiden t som

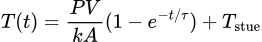hvor

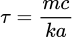er en karakteristisk tid.

Et teori, et andet praksis

Som du nok kan se, er der mange faktorer at tage hensyn til. For eksempel afhænger konvektionstabet også af, om du holder pappet lodret eller vandret. Derfor foreslår Lars, at du laver et eksperiment og måler pappet overfladetemperatur.

Som du selv er inde på, kræver det noget udstyr, der ikke er standard i køkkenet, nemlig et infrarødt termometer. Men jeg kan google mig til, at sådan nogle kan fås helt ned til omkring 250,- kr.

Så nu ved du hvad du skal ønske dig til jul :)

Bedste hilsener,
Peter Laursen, Astrofysiker og videnskabformidler på Cosmic Dawn Center