Spring i kørende tog
Hej Spørg om Fysik
Studerende på Ribe Katedralskole: Jeg har gået og reflekteret lidt over fysikkens love i kørende tog, siden jeg på YouTube stødte på et klip, hvor nogle unge mennesker 'flyver' på en brændslukker, efterfulgt af ordene 'movement in a train against its driving-direction will increase the lenght of the movement' - eller noget i den stil.
Altså - når jeg hopper fremad i et tog, der kører mod mig, hopper jeg længere (?). Så kom jeg til at tænke på - hvorfor flytter jeg mig egentlig ikke, når jeg hopper opad i et tog? Hvordan hænger bevægelse og kraft egentlig sammen i et kørende tog? Og hvad med tryk og acceleration - hvilke roller har disse faktorer?
Håber på et svar snarest muligt!
Med venlig hilsen
A I

Når du står i et tog der bevæger sig retlinet med konstant hastighed, og springer fra et givet sted, er dit spring præcist lige langt (så langt som du nu kan) uafhængigt af om du springer i togets bevægelsesretning eller imod bevægelsesretningen målt i toget.
Prøv selv! Det er rigtigt, at set fra det ubevægelige jordsystem kommer du længere, når du springer i samme retning som toget bevæger sig, end når du springer imod togets bevægelsesretning. Når man transformerer fra et koordinatsystem der ligger stille, til et der bevæger sig langs x-aksen af det stillestående system med hastigheden v, har man en transformationsligning, dvs. en ligning der kan overføre bevægelsen i det ene system til det andet, som siger:
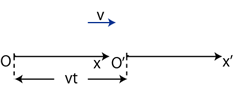
Transformation imellem to koordinatsystemer
x = x’ +v*t og u = u’ +v, hvor de umærkede koordinater er i det stillestående system, og de mærkede i det bevægede system, x og x’ er koordinaterne i de to systemer samt u og u’ er hastigheden af en genstand i det faste henholdsvis det bevægede system. I begge systemer er der samme tid t (når det kun er langs x-aksen kan vi sige farten, den er så positiv i retningen af den positive x-akse).
Eksempel: et tog kører med 30 m/s og et hop skråt op med 6,5 m/s i en vinkel på 30 grader. Det giver i toget en hoppelængde på omkring 3,7 m. Man er i luften ca. 1,3 sek. Set fra jorden får man for startstedet, som har x’ = 0 m og t = 0 sek., sætter x = 0 m. For landingsstedet set fra jorden, får man ca. x = 3,7 m + 30 m/s * 1,3 s = 42,7 m (pænt spring men springhastigheden set fra jorden er også u = 35,6 m/s vandret). Springer man imod togets bevægelsesretning giver tilsvarende regning x= -3,7 m + 39 m = 35,3 m i togets bevægelsesretning. Det er stadig et langt spring men kortere end før.

Spring fra kørende tog
Her er det forudsat, at toget ikke accelererer - gør det det, kan man lave tilsvarende beregninger, så den eneste acceleration der indgår her er tyngdeaccelerationen, som er den samme på jorden og i toget. Trykket kommer ikke ind på nogen måde, som jeg kan se.
Med venlig hilsen
Malte Olsen
