Vejer man mindre ved ækvator?
Hej Spørg om Fysik
Jeg har et spørgsmål om vægt. Jeg har hørt, at et menneske skulle veje mindre ved ækvator end i Danmark, på grund af centrifugalkraften, er det rigtigt, og isåfald hvor meget?
På forhånd tak
Med venlig hilsen
G N
En persons masse er konstant (i det mindste i korte perioder), og den måles i kg. Vægten eller kraften vi bliver påvirket fra jorden med, er varierende efter breddegraden. Den er højst ved polerne og mindst ved ækvator.
Dette skyldes 2 forhold. Ved ækvator er der 6378 km til jordcenteret, og ved polerne er der 6357 km til jordens centrum. Tyngdekraften aftager med kvadratet på afstanden fra jordcenteret, og det giver en lille virkning. Vægten ved jordcenteret/vægten ved polerne får af denne grund altså en forskel på (6357/6378)2 = 0,9934. Dette betyder, at vejer man 75 kg på nordpolen, så vil man veje 74,6 kg ved ækvator.
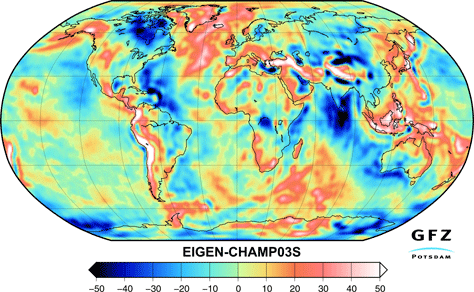
Verdenskort der viser tyngdeaccelerationens variation. Enhederne i målestokken er på 3 cifre efter kommaet. Der henvises til Potsdam, som har været referencepunkt i mere end 100 år.
Så ja, det er rigtigt, at man vejer mindre ved ækvator end ved nordpolen. Desuden, som spørgeren skriver, er der behov for en mindre centripetalkraft ved ækvator.
Forholdet kan bedst beskrives ved hjælp af tyngdeaccelerationen, g. Ved polerne er g = 9,832 m/s2, i Danmark på 55 ° bredde er g = 9,815 m/s2, ved ækvator er g = 9,780 m/s2. Vores person på 75 kg trykker altså på en vægt med kraften F = m*g, som ved polerne giver en vægt på 75 kg * (9,832/9,815) = 75,13 kg, ved ækvator bliver det så 75 kg*(9,780/9,815) = 74,73 kg. Altså vejning ved polerne giver ca. 400 g mere end vejning ved ækvator.
Bidraget fra rotationen kan udregnes til ca. 1,4 g ved ækvator, og ved anvendelse af formelen for centripetalkraften, så det er ikke den afgørende faktor, men den er der. Den større radius er naturligvis en konsekvens af rotationen, så indirekte har rotationen skylden for en stor del af forskellene.

Lodvægt som vil vise samme masse overalt da lodderne påvirkes akkurat som personen
Der er forskel på vægte
Nu er det ikke ligegyldigt, hvilken vægt man vejer sig på. Skal man se denne forskel, kræver det, at det er en fjedervægt eller tilsvarende man vejer sig på - (alle de almindelige personvægte af den flade type, der står på gulvet, er af den type, det er en kuffertvægt også).
Vejer man sig derimod på en lodvægt, dvs. hvor man flytter lodder på en vægtskål, og står på den anden vægtskål selv, vil vægten være konstant, uanset hvor man er, fordi lodderne påvirkes på præcis samme måde som personen. Det er den type vægte, hvor man har en opstander, og står og forskyder lodder eller en gammeldags ballance vægt. Tyngdeaccelerationen afhænger også af højden over jordoverfladen, den aftager med afstanden til jordcenteret.

Personvægt af fjedertypen som vil vise forskelligt på nordpolen og ækvator
Størrelsesordenen er, at g bliver mindre, og det kan groft udregnes til en ændring på g på -0,00000308 * h, hvor h måles i meter over 0 meter. Så ønsker man sig at blive lidt lettere, kan man gå op i en skyskraber, f.eks. verdens vist højeste Burj Khalifa i Dubai, på 828 meter. Det giver så en g, der er 0,00255 m/s2 mindre eller i størrelsesorden 0,3 promille. Skal man rigtigt glæde sig over det, skal det være i et fly i 10 km højde, hvor man kommer op omkring 3 % eller lidt over 2 kg, men det er jo sjældent, at man vejer sig ombord på et rutefly. Toppen på Mount Everest er i øvrigt ligeså god.
I princippet påvirker solen og månens stilling, i forhold til vægten, også forholdene, men det er forsvindende lidt. Ved at måle g meget præcist kan man i øvrigt vurdere, om der er metallejer, olie etc. nær jordoverfladen, så det er en af de teknikker man kan bruge til kortlægning af grundstofreserverne på jorden, men en variation siger naturligvis ikke hvad der er under jorden.

Verdens højeste bygning Burj Khalifa i Dubai, på 828 meter
Denne metode anvendes iøvrigt også til at søge efter u-både i oceanerne.
Her er så ikke taget højde for luftens opdrift
Kold luft har større densitet end varm luft, og giver derfor større opdrift dvs. der er mindre opdrift fra den antageligt varme luft ved ækvator end ved på polerne, hvor der er koldt. Opdriften på vor 75 kg lette person er i størrelsesorden 97 g ved normalt tryk og temperatur 0° C . Ved polerne er den omkring 109 g (1 atm. og – 30 °C) ved ækvator (1 atm. +40 °C) ca. 64 g, altså her en forskel på ca. 45 g fra opdriften i den modsatte retning.

Moderne mikroanalysevægt, sidste ciffer er 0,0000001 g
Skal man veje meget præcist, må man tage opdriften med i beregningen, og sørge for, at der ikke er elektrostatiske ladninger, som tiltrækker eller frastøder hinanden omkring vægten, ikke er magnetiske kræfter osv.
Med venlig hilsen
Malte Olsen
