Hvad sker der med en kugle, som skydes lige op i luften?

Svar:

Hej Tonny,

Hvis vi ser bort fra vindmodstanden er svaret trivielt: Kuglen starter med en vis kinetisk energi, som alt sammen konverteres til potentiel energi når den når sin maksimale højde, hvorefter det konverteres tilbage til den samme mængde kinetiske energi. Hvis kuglen starter med 900 m/s, ender den derfor også med 900 m/s.

Det ved du jo sikkert godt, og tænker formodentlig, hvordan tager vi højde for vindmodstanden?

Er du slet ikke interesseret i detaljerne, kan du scrolle ned til bunden. Men vil du forstå lidt om, hvordan vi kan sige noget om kuglens bane og hastighed, så læs med:

Vindmodstand

Som du ved fra cykelstien, stiger vindmodstanden hurtigt med farten (v). Mere præcist stiger den med kvadratet på farten, dvs. farten i 2. potens. Den stiger også med dit tværsnitsareal, A, hvilket er grunden til, at det kan betale sig at krumme dig sammen og iføre dig det strammeste sæt spandex, du kan få på. Derudover stiger den med luftens tæthed, ρ, som er ret konstant, men alligevel f.eks. er en anelse højere for kold luft end for varm, hvilket betyder, at det er lidt hårdere at cykle om vinteren end om sommeren. Den falder også med ca. 1% for hver 80 meter, du kommer op, og afhænger tillige af, om der er højtryk eller lavtryk. Men lad os se bort fra dét.

En typisk kaliber for en riffel er det, der hedder "7.6 mm", men det refererer til den indre diameter, hvor den ydre er omkring 7.8 mm. Kuglens tværsnitsareal er altså A = π × (7.8 mm/2)² = 0.48 cm². For luftens tæthed kan vi tage ρ = 0.0012 g/cm³.

Den sidste ting, som har indvirkning på vindmodstanden, er den såkaldte "vindmodstandskoefficient", eller "luftmodstandskoefficient", som betegnes c_d. Dette tal beskriver, hvor meget "modstand" et objektet yder mod luften. Det er typisk af størrelsesordenen 1, og et lille tal betyder at vinden ikke "griber så meget fat" i objektet, mens et stort tal betyder meget modstand. Altså, jo mere aerodynamisk objektet er, jo mindre er c_d.

Luftmodstandskoefficienten er ikke konstant for et objekt, men afhænger også af, præcis hvordan luften flyder forbi, f.eks. hvor hurtigt, og om der er turbulens eller laminart flow. Det er generelt noget, som må bestemmes eksperimentelt. I tabellen her kan du se nogle forskellige værdier:

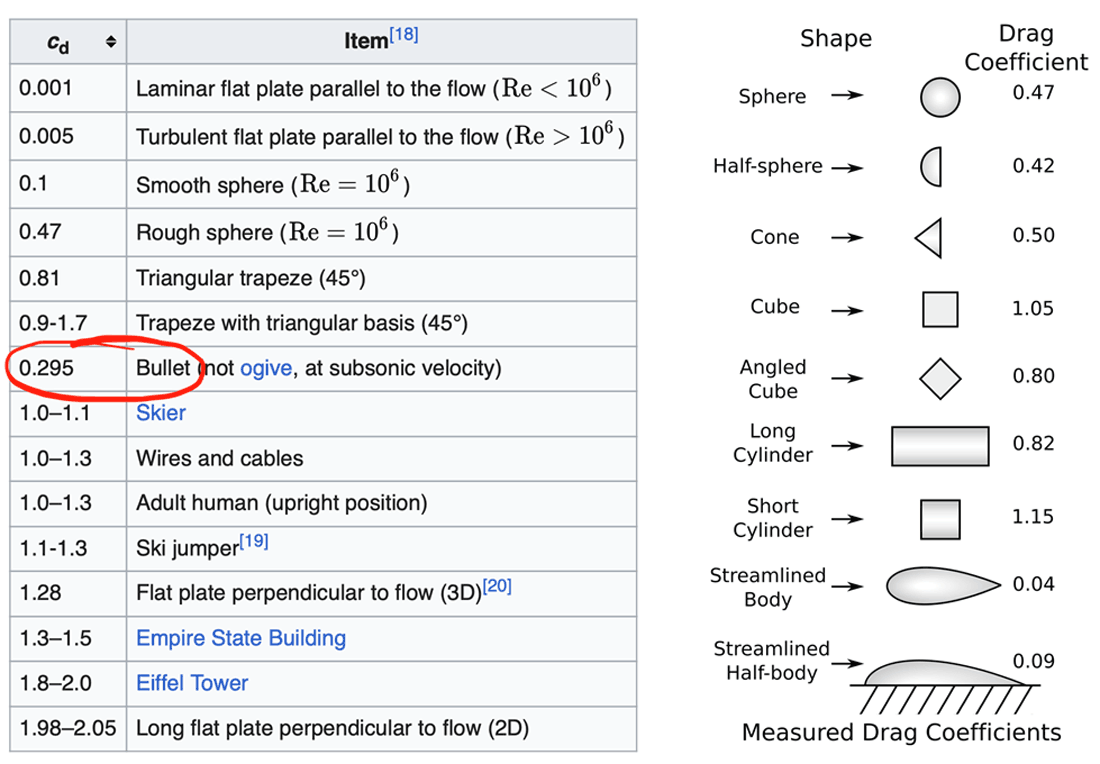
Som du kan se i tabellen, har en kugle fra en riffel eller pistol omtrent c_d = 0.3.

Maksimal højde

Vi er nu klar til at beregne luftmodstanden, som er en kraft, der er givet ved

F_d  =  ½ ρ c_d A v²,

hvor subscriptet d står for "drag". Kuglen starter ved v₀ = 900 m/s, men decelererer, så v falder. Denne deceleration, som altså er en negativ acceleration der kan skrives a = dv/dt, skyldes to ting, nemlig Jordens tyngdekraft mg, hvor g = 9.81 m/s² er tyngdeaccelerationen, og luftmodstanden F_d.

Dvs. at den samlede kraft, som virker på kuglen, er

F_tot  =  F_g + F_d,

eller

m dv/dt  =  –mg – ½ ρ c_d A v².   (ligning 1)

Resultatet er, at kuglen når op i en højde på knap 2.9 km (for m = 12 g og v₀ = 900 m/s).

Dette er en noget idealiseret beregning, men det er ikke helt ved siden af. Ifølge disse detaljerede beregninger referereret på Close Focus Research når et 7.6 mm-projektil en højde på mellem 2400 m og 3000 m, alt efter den præcise type.

Kuglens endelig hastighed

Efter at have nået sin maksimale højde, vil kuglen begynde accelerere nedad, indtil luftmodstanden opvejer tyngdekraften, hvorefter den vil falde med konstant hastighed. Ved denne såkaldte "terminalhastighed", v_t, er accelerationen altså 0, så fra ligning (1) fås, at

v_t  =  √(2mg / ρAc_d)

Hvis vi putter værdierne for de forskellige konstanter ind, får vi, at kuglen når en max-hastighed på v_t = 117 m/s, eller godt 420 km/t.

Men når kuglen begynder at falde tilbage igen, vil den ikke nødvendigvis længere holde sin retning med spidsen forrest, men kan i stedet tumle ned. Det afhænger vist lidt af, hvordan projektilet er konstrueret. Dette øger luftmodstandskoefficienten, både fordi det effektive tværsnitsareal stiger, og fordi luftmodstandskoefficienten stiger. Jeg ved ikke præcis til hvad, men hvis de begge stiger 50% eller 100%, kommer der hhv. en faktor 2.25 eller 4 i nævneren inde i kvadratroden, i hvilket tilfælde max-hastigheden bliver hhv. ca. v_t = 80 m/s (280 km/t) eller 60 m/s (210 km/t).

Eksperiment (don't try this at home!)

Det præcise tal kan næppe udregnes, men må findes eksperimentelt. Det er ikke let, for en kugle der skydes flere kilometer op i luften, ryger sjælden ned samme sted. Retter man geværet 89° opad i stedet for 90°, får kuglen en vandret hastighed på 900 m/s × cos(89°), dvs. knap 16 m/s. Det tager kuglen godt 30 sekunder at vende tilbage (beviset efterlades som en øvelse for læseren), og i denne tid har den så rejst over en halv kilometer — i en tilfældig retning.

Men selv hvis man skød 90.0000° opad, kan man ikke se bort fra sidevind. Selv på en vindstille dag, kan der være betragtelig vind i et par kilometers højde

I 1920 udførte en delegation af den amerikanske hær, U.S. Army Ordnance, nogle forsøg, hvor de skød forskellige kugler op fra en platform i en sø, og lyttede efter, hvornår de kunne høre et plask. De fandt, at det tog 49 sekunder for 7.6 mm kugle (dog lidt lettere, 9.7 gram) at returnere, og at dens hastighed ved nedslag var 300 fod/s, dvs. ca. 90 m/s eller 330 km/t.

MythBusters udførte i et afsnit et forsøg på et stort, fladt område i Mojaveørkenen i sydvest-USA, hvor de skød forskellige projektiler op i luften fra en pistol og bagefter gennemsøgte området.

De fandt to af kuglerne i ~100 meters afstand og kunne ud fra hullerne i jorden se, at kuglerne var faldet sidelæns med en "ikke-dødelig hastighed"; omkring 45 m/s, eller 165 km/t, som passer med nogle forsøg i en vindtunnel, de også foretager. Det samme viste nogle kugler, som de lod falde fra en ballon i 400 fods højde, mens de ikke kunne finde nogle af de kugler, de affyrrede med en riffel.

Men… som de selv nævner, har der altså været flere ulykker, hvor mennesker er blevet dræbt af nedfaldende kugler (se f.eks. Wintemute et al 2012), så jeg ved ikke hvor meget vi skal lægge i deres resultater.

Bedste hilsener,
Peter Laursen, astrofysiker og videnskabsformidler,
Cosmic Dawn Center, Niels Bohr Institutet.