Projection Noise
Even when ν clock and ν osc are exactly identical sometimes we find more atoms in ↑ (and sometimes more in ↓ ).
IfΔν=0 after all the microwave pulses every single one of theN a =100000 atoms is in the quantum state
so that for each atom there is an equal chance of finding it in↑ or↓ .
But as in tossing a coin 100000 times only on average we find 50000 heads and 50000 tails. From statistics we know that in this case var(N ↑ −N ↓ )=N a . This is the projection noise.
If we add the Bloch-vectors of every atom to form a big vector with length N a the total vector has an associated uncertainty which can be represented as probability distribution on the sphere.
Using this picture the whole Ramsey-spectroscopy sequence can be summed up in one picture: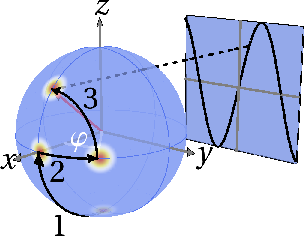
The uncertainty with which we can estimate the precession angle φ is δφ=1 N a √ .
Since φ=Δν⋅τ , for an interrogation time τ this means that we can measure the frequency with a precision δν=1 τN a √ .
- Using more atoms (performing more measurements simultaneously) is one way to increase the precision.
- A longer interrogation time τ increases the precision of frequency measurements (but not of phase measurements).
- We can use entanglement to reduce the phase fluctuations.
