Quantum measurement and control of mechanical states
of the world, the act of measurement assumes a special role, not least due to its inevitable “backaction” on the measured system. The associated questions become particularly intriguing when studied with objects visible to the naked eye.

A quantum measurement is then one for which the measurement backaction is not obscured by other sources of noise. In case of an optical readout of mechanical motion, this means that the light should interact strongly with the mechanics, in particular at a rate larger than the two decay rates to their respective thermal environments.
If the measurement is also efficient enough (in the sense of information gained per backaction imposed), its record can be used to predict and “retrodict” the quantum state of motion of the (mechanical) system.
In particular, with such quantum measurements at hand, we can perform quantum feedback on the mechanical state and prepare macroscopic mechanical systems in their quantum ground state.
Noise-cancelling headphones rely on essentially the same feedback, the distinction being that our measurement is so near-ideal that we can tamp down the quantum noise. Check out the following link for a nice elaboration of this analogy by a former postdoc in our group, David Mason.
From his review, we here underline one interesting fundamental question at the intersection of gravity and quantum mechanics, which could be probed owing to the fact that our macroscopic mechanical system can definitively be treated as quantum: if one could place a mechanical object into a quantum superposition (in two places at the same time), would it gravitationally interact with itself?
Note that this research was conducted at cryogenic temperatures (~4 K). In that sense, it combines aspects of experimental and theoretical quantum optics and optomechanics, quantum measurement and quantum control theory, while making use of electronics, vacuum systems and cryogenic systems.

…now (almost) available also at room temperature!
That said, we are also putting a lot of effort into the development of novel optomechanical systems with the idea of doing the same physics at room temperature (RT). At RT, mechanical losses become more significant, as does the occupancy of the mechanical thermal bath, both of which means the requirement for having a quantum measurement becomes more challenging. Our systems are already at the cusp of being of high enough quality even in this scenario. The prominent trait of the newly developed system is then that it exhibits sufficiently low frequency noise at the frequency region of interest (i.e. that of the addressed membrane mode). In particular, to achieve this, the optical subsystem is composed of a fiber mirror (which is so small that its vibrational modes are much higher in frequency) and a special mirror with a silicon supporting structure on its back (designed to create a bandgap around the membrane mode, in a similar fashion the pattern of holes in the membrane creates a bandgap in its spectrum). We are currently working towards ground-state cooling of the membrane mode at RT (present level is ~20 phonons, owing to residual mirror frequency noise and feedback filter imperfections). A future goal would also be generating entanglement between two membrane modes at RT.
Quantum correlations and entanglement in optomechanical systems
The optomechanical interaction creates correlations, all the way down to the quantum fluctuations in the light and the motion. We can thereby also generate entanglement—the key resource for many quantum technologies—in an optomechanical system.
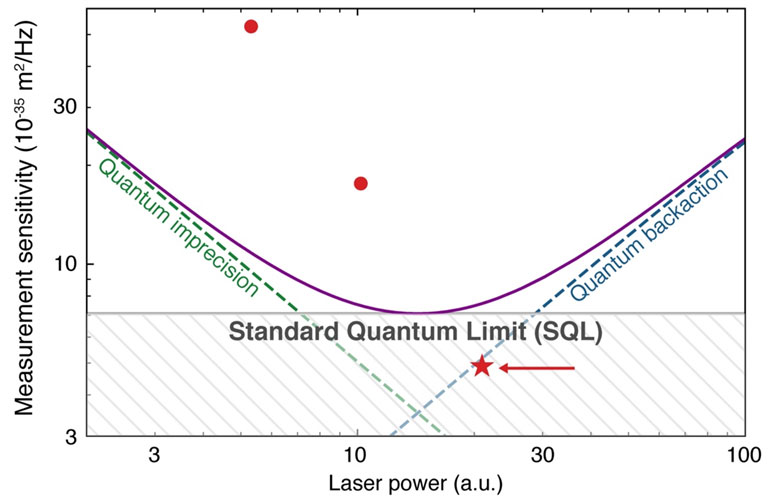
We study these quantum correlations and seek to harness them for quantum sensors—including gravitational wave observatories such as LIGO—and quantum information processing. Specifically, in the context of interferometric displacement measurements, the quantum imprecision and quantum backaction result in the so-called standard quantum limit (SQL), at which the combined effect of the two is minimised. The SQL is customarily formulated under the assumption that the imprecision and backaction noises are uncorrelated and, as such, does not constitute a fundamental quantum limit. Indeed, correlations between the two exist whenever backaction-dominated motion (arising from amplitude fluctuations of the optical field) is imprinted into the phase fluctuations of the same field. One then only needs to measure a mixed quadrature of the field. Again, the measurement should exert strong backaction, and should also be efficient enough, as any optical losses spoil the desired destructive interference by substituting uncorrelated vacuum noise. We were recently able to exploit these correlations in our optomechanical system to demonstrate measurements of force and position with a sensitivity better than the SQL, but also to generate entanglement of optical fields of very different frequencies. Tailoring entanglement and correlations in complex multimode systems and practical sensing settings, including room-temperature conditions, is a goal of future research.
Similar to that above, this research combines aspects of experimental and theoretical quantum optics, optomechanics and quantum information, as well as electronics, vacuum systems and cryogenic systems.
